Previous: Theory 9 to Endgame
PLEASE READ GENERAL GUIDE PAGE BEFORE READING THIS
WIP THIS INFORMATION IS NOT PROOFREAD AND MAY BE INACCURATE
Disclaimer: This is a simplified version of the guide. The guide will skip over things, and is not completely optimal. Click here for a more polished, in-depth, and optimal guide.
When discussion strategy, this section may use more jargon then the rest of the guide. If you are confused, please check out the discord server and ask.
Weierstraß sine product (WSP)
- Sim time to completion: 4 years and 333 days
- Dev: Xelaroc
- Milestone route: 0/0/3 → 0/1/3 → 4/1/3
- One sentence description: TBA
WSP overview:
WSP is based of of Weierstrass' sine approximation: \(s_n(x) = x \Pi_{k=1}^n(1 - (\frac{x}{k\pi})^2)\).
The capital pi notation, as in student and tau calculations means to multiply all the terms together, like sigma notation but for
multiplication.
The product looks scary but it simply defines a function \(s_n\) that approximates sine. The higher \(n\) values you pass into it, the better the
approximation it. Essentially, as n goes to infinity, \(s_n(x)\) approaches sin(x)
However, \(s_n(x)\) is quite inaccurate, and for large values of x, \(s_n(x)\) is much larger/smaller then sin(x), even for large values of n.
for instance. Essentially, as x gets bigger, \(s_n(x) / sin(x)\) gets bigger, very fast, even for large values of n
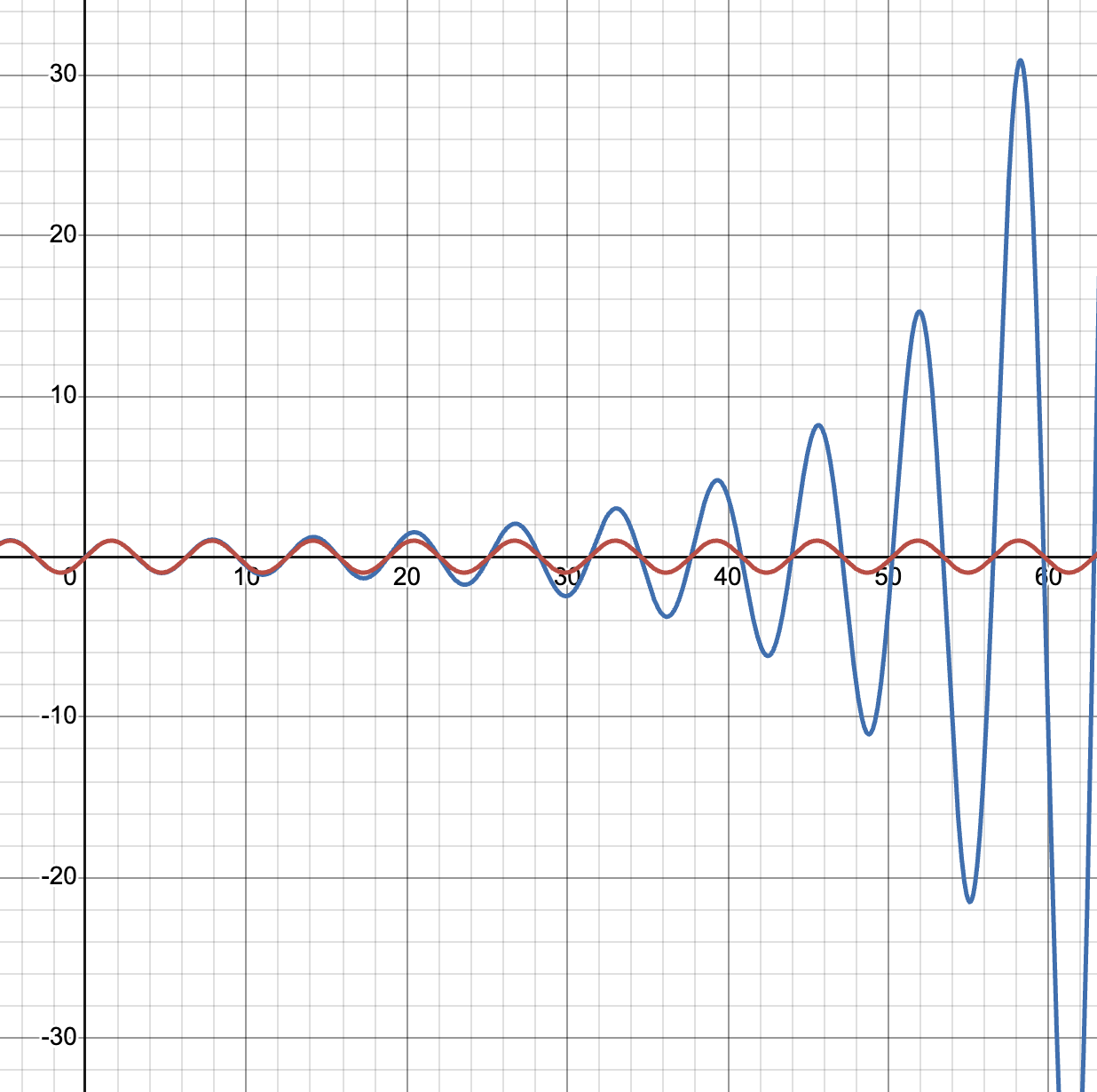
red: sin(x), blue: \(s_{100}(x)\)
This theory exploits this inaccuracy, and uses it to increase \(\rho\)
Equation breakdown
\(\dot{\rho} = q_1q_2q\)
\(\dot{q} = c_2\frac{s_n(\chi)}{sin(\chi)}\)
\(\chi = \pi \frac{c_1n}{c_1 + n / 3^3} + 1\)
These equation shows that to increase \(\rho\) you want to increase q
To increase q you want to increase \(s_n(\chi) / sin(\chi)\), which is the stirling approximation from earlier. Thus to increase \(s_n(\chi) / sin(\chi)\), you want to increase \(\chi\), and decrease n
The third line shows how to increase \(\chi\). It is based off of n and \(c_1\). Generally, the boost to \(\chi\) you get from increasing n outweighs that decrease in \(s_n(\chi) / sin(\chi)\) increasing n would cause. Therefore, n is overall positive
\(c_1\) lategame out-competes n in the denominator, meaning over time it gets weaker and weaker compared to n\(^{[why?]}\)
And thus we have the variable breakdown:
| \(q_1\) | Increases \(\dot{\rho}\) directly by approx 7% |
| \(q_2\) | Increases \(\dot{\rho}\) directly by 2x |
| \(c_1\) | Increases \(\chi\) (affect changes over time) |
| \(n\) | Increases \(\chi\) (affect changes over time) |
| \(c_2\) | Increases \(\dot{q}\) by 2x |
\(c_1\) and \(n\) affect \(\dot{\rho}\) differently over time
| \(c_1\) | Initially 50% increase in q. Decreases to 0 over time. Negligible after 1e400 |
| \(n\) | Initially 50% increase in q. Increases to 4x over time. Almost 4x after 1e400 |
Optimal publication multiplier:
- 0 - e50: 2 - 4
- e50 - e75: 5 - 7
- e75+: ~8
Strategies:
The best strategy for WSP is always WSPdStopC1. This strategy changes to accommodate that changing power of \(c_1\) and \(n\). However, to
simplify, I have a different strat written here: WSPdStopC1noMod. This is not a mainstream strat, so people may not know what you're talking
about and the sim will not recommend it. The sim will recommend WSPdStopC1 instead.
WSPdStopC1
WSPdStopC1noMod
| var | First 15s | Rest of pub |
|---|---|---|
| \(q_1\) | Always buy | When cost is \(\frac{1}{10}\) of \(min(q_2, n, c_2) cost\) |
| \(q_2\) | Always buy | Always buy |
| \(c_1\) | Always buy | When cost is \(c_1\) ratio cheaper then \(min(q_2, n, c_2) cost\) |
| \(n\) | Always buy | Always buy |
| \(c_2\) | Always buy | Always buy |
\(c_1\) ratio
- 0 - e25 \(\rho\): 1
- e25 - e40 \(\rho\): 3
- e40 - e200 \(\rho\): 10
- e200 - e400 \(\rho\): 50
- e400 - e700 \(\rho\): 1000
- e700+: Don't buy c1 more then 15 seconds into the publication
The idle strat for WSPdStopC1 is WSPStopC1 (no d), which is slightly different from just autobuying all except those listed as never buy
✔️ - Always buy, ❌ - Never buy
WSPStopC1
| var | First 15s | Rest of pub |
|---|---|---|
| \(q_1\) | ✔️ | ✔️ |
| \(q_2\) | ✔️ | ✔️ |
| \(c_1\) | ✔️ | ❌ unless \(\rho\) < 1e450 in which case ✔️ |
| \(n\) | ✔️ | ✔️ |
| \(c_2\) | ✔️ | ✔️ |